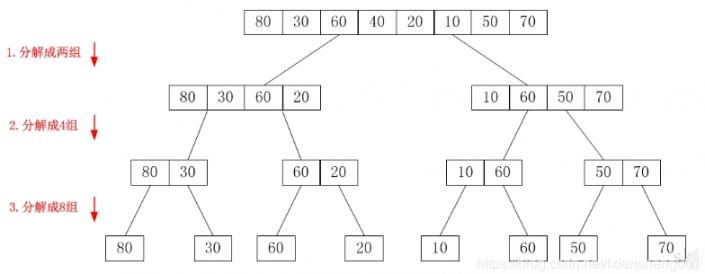
归并排序

 * 归并排序：时间复杂度T(N) = a*T(N/b) + O(N^d) 
 *       log(b,a) = d=1 --> 复杂度为O(N^d * logN) -->O(n*logn)
 *       空间复杂度O（n)
 * 稳定性：不会交换相同数的位置，是一个稳定方法

话不多说，直接上代码：

public class MergeSort {

	public static void mergeSort(int[] arr,int L,int R){
//		如果数组就还剩一个数，弹出；
		if(L==R){
			return;
		}
//		获取中点  mid= L + (R-l)/2   防止下标溢出
		int mid =(L+R)/2;
//		对左半部分进行归并：分解
		mergeSort(arr,L,mid);
//		对右半部分进行归并：分解
		mergeSort(arr,mid+1,R);
//		调用真正的排序方法：合并
		sort(arr,L,mid,R);
	}
	public static void sort(int[] arr,int L,int mid,int R){
//		创建一个辅助数组；这里应该是R-L+1表示的是仅本次执行的数量个数。
		int[] help=new int[R-L+1];
//		作为辅助数组的下标
		int j=0;
//		作为判断以及赋值的下标
		int p=L;
//		作为判断以及赋值的下标
		int q=mid+1;
//		
		while(p<=mid&&q<=R){
			help[j++]=arr[p]>arr[q]?arr[p++]:arr[q++];
		}
//		如果p不满足条件，说明q已经执行完毕，只剩下p对应的数组，直接将剩下的进行赋值
		while(p<=mid){
			help[j++]=arr[p++];
		}
//		如果p不满足条件，说明q已经执行完毕，只剩下p对应的数组，直接将剩下的进行赋值
		while(q<=R){
			help[j++]=arr[q++];
		}
//		将结果放到最后的数组中。
		for(int i=0;i<=help.length-1;i++){
			arr[L+i]=help[i];
		}
		
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
//		初始值
		int[] arr = {1,3,5,7,9,2,4,6,8};
//		调用方法
		mergeSort(arr,0,arr.length-1);
		for (int i : arr) {
			System.out.println(i);
		}
	}

}

具体执行过程如下图所示：注意递归的跳转

递归完全铺开的示意图如下